paperlined.org
dev > oss > high_energy_slings
document updated 10 years ago, on Jun 16, 2014

What is the best launch angle, when trying to maximize projectile range?

If sling length is kept constant, then the classic answer is 45°.

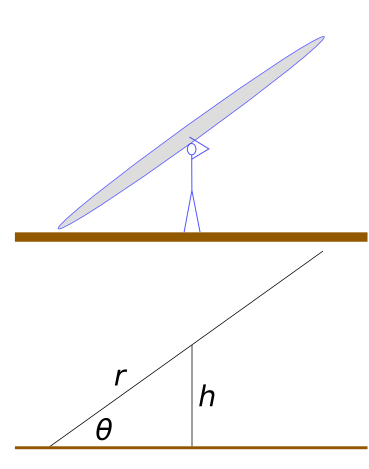
However, if sling length is chosen to be as long as possible, just short of dragging on the ground, then sling length varies with launch angle (assuming helicopter style, on flat ground). With low launch angles, sling length can be much longer. So launch velocities increase with decreasing launch angle.

How does a varying launch velocity affect the optimum launch angle?

Calculations

Our goal here is to calculate projectile range as a function of launch angle.

We have two different equations for projectile energy: $$ E = {1 \over 2} r F$$ $$ E = { mgd \over 2 sin(2 \theta) } $$

Combine them, and solve for \(d\): $${ mgd \over 2 sin(2 \theta) } = {1 \over 2} r F$$ $$ d = {1 \over 2 g} \cdot {r F \cdot 2 sin(2\theta) \over m}$$ $$ d = {1 \over g} \cdot {r F \cdot sin(2\theta) \over m}$$

The sling length for this launch angle is: $$sin(\theta) = {h \over r}$$ $$r = { h \over sin(\theta) }$$

Where \(h\) is the height of the handle, and \(r\) is the sling length (radius).

Plug that into the distance equation: $$ d = {1 \over g} \cdot {h F \cdot sin(2\theta) \over m d \cdot sin(\theta)}$$

For graphing purposes, we'll arbitrarily choose these parameters:

Conclusion

This suggests that the best launch angle is very near 0°. In other words, use as long of a sling as possible.

Practicalities — sling length

As launch angle approaches 0°, sling length approaches infinity. In real-world testing, it has proven extremely difficult to use sling lengths greater than 20 feet. So the above graph is unrealistic in the region of ≤15°.

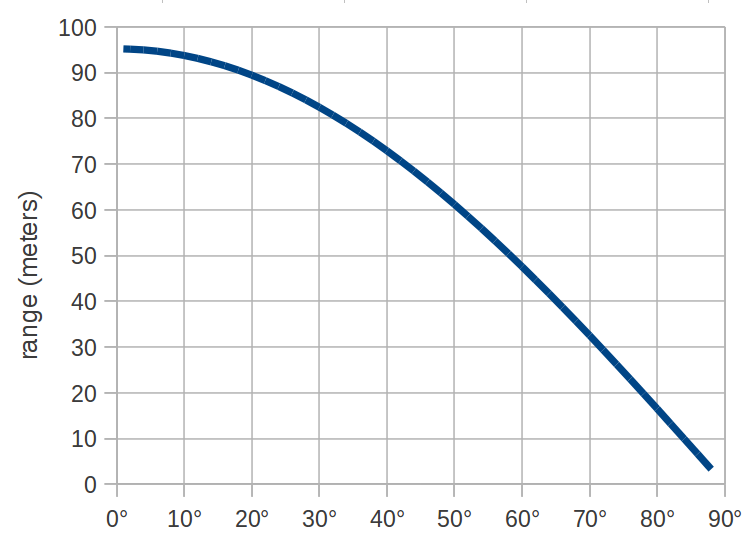
So the answer to "how long should my sling be?" is "as long as is practical".

Practicalities — air resistance

The above equation ignores air resistance. This has a large impact on the conclusions drawn here, because the graph highlights the region with the highest launch velocity, and drag has a bigger effect at higher velocities.

Diminishing returns

The conclusion is that the longer the sling, the better. However, as launch angle approaches 0°, the range approaches an asymptote. This is because:

$$ \lim_{\theta \to 0} {sin(2\theta) \over sin(\theta)} = 2 $$

So the asymptote (the maximum possible range) is:

$$ d = {1 \over g} \cdot {F \cdot h \over m} \cdot 2 $$

In practical terms, the curve flattens out very near 0°. Which means that if you're struggling to use a 40 foot sling instead of a 30 foot sling, don't worry about it, because the extra 10 feet isn't going to help your range very much.